RE中的常见加密算法

Base64

参考材料: Base64加密算法以及在IDA中的识别

Base64是一种基于64个可打印字符来表达二进制数据的表示方法. 由于2的6次方等于64, 所以每6个比特为一个单元.

3个字节有24个比特, 在Base64中6个比特一个单元, 所以对应着4个Base64单元, 也就是3个单元(字节)可由4个可打印字符来表示.

base64_0

base64_1

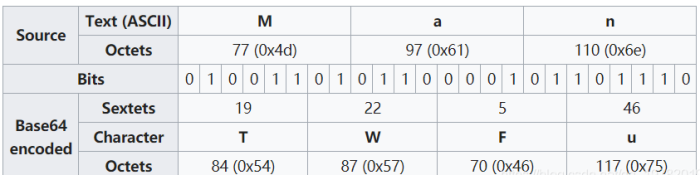
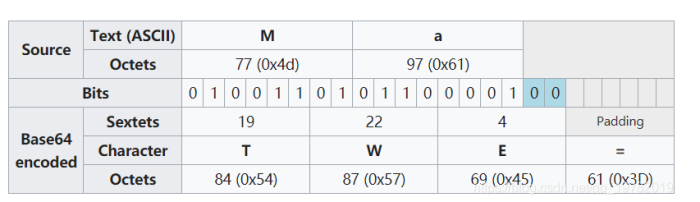
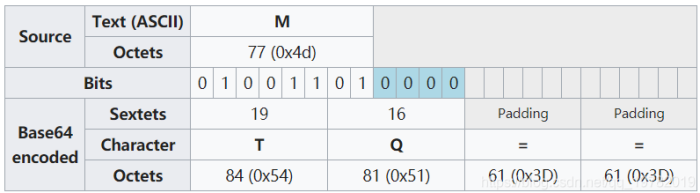
若是一组中少一个字符, 则用一个”=“添加在末尾; 若是缺两个字符, 则用两个”=“来填充

base64_2

base64_3

C程序代码实现:

1
#include <stdio.h>
2
#include <stdint.h>
3
#include <stdlib.h>
4
#include <string.h>
5

6
const char base64_table[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
7

8
int base64_reverse_table[256];
9

10
void build_reverse_table() {
11
    for (int i = 0; i < 256; i++) {
12
        base64_reverse_table[i] = -1;
13
    }
14
    for (int i = 0; i < 64; i++) {
15
        base64_reverse_table[(unsigned char)base64_table[i]] = i;
59 collapsed lines
16
    }
17
}
18

19
// Base64 编码
20
char* base64_encode(const unsigned char* data, size_t input_length) {
21
    size_t output_length = 4 * ((input_length + 2) / 3);
22
    char* encoded_data = (char*)malloc(output_length + 1);
23
    if (!encoded_data) return NULL;
24

25
    for (size_t i = 0, j = 0; i < input_length;) {
26
        uint32_t octet_a = i < input_length ? data[i++] : 0;
27
        uint32_t octet_b = i < input_length ? data[i++] : 0;
28
        uint32_t octet_c = i < input_length ? data[i++] : 0;
29

30
        uint32_t triple = (octet_a << 16) | (octet_b << 8) | octet_c;
31

32
        encoded_data[j++] = base64_table[(triple >> 18) & 0x3F];
33
        encoded_data[j++] = base64_table[(triple >> 12) & 0x3F];
34
        encoded_data[j++] = base64_table[(triple >> 6) & 0x3F];
35
        encoded_data[j++] = base64_table[triple & 0x3F];
36
    }
37

38
    // Add padding
39
    for (size_t i = 0; i < input_length % 3; i++) {
40
        encoded_data[output_length - 1 - i] = '=';
41
    }
42

43
    encoded_data[output_length] = '\0';
44
    return encoded_data;
45
}
46

47
// Base64 解码
48
unsigned char* base64_decode(const char* data, size_t* output_length) {
49
    size_t input_length = strlen(data);
50
    if (input_length % 4 != 0) return NULL;
51

52
    *output_length = input_length / 4 * 3;
53
    if (data[input_length - 1] == '=') (*output_length)--;
54
    if (data[input_length - 2] == '=') (*output_length)--;
55

56
    unsigned char* decoded_data = (unsigned char*)malloc(*output_length + 1);
57
    if (!decoded_data) return NULL;
58

59
    for (size_t i = 0, j = 0; i < input_length;) {
60
        uint32_t sextet_a = data[i] == '=' ? 0 & i++ : base64_reverse_table[(unsigned char)data[i++]];
61
        uint32_t sextet_b = data[i] == '=' ? 0 & i++ : base64_reverse_table[(unsigned char)data[i++]];
62
        uint32_t sextet_c = data[i] == '=' ? 0 & i++ : base64_reverse_table[(unsigned char)data[i++]];
63
        uint32_t sextet_d = data[i] == '=' ? 0 & i++ : base64_reverse_table[(unsigned char)data[i++]];
64

65
        uint32_t triple = (sextet_a << 18) | (sextet_b << 12) | (sextet_c << 6) | sextet_d;
66

67
        if (j < *output_length) decoded_data[j++] = (triple >> 16) & 0xFF;
68
        if (j < *output_length) decoded_data[j++] = (triple >> 8) & 0xFF;
69
        if (j < *output_length) decoded_data[j++] = triple & 0xFF;
70
    }
71

72
    decoded_data[*output_length] = '\0';  // Optional for text
73
    return decoded_data;
74
}

TEA

参考资料: TEA/XTEA/XXTEA系列算法

TEA（Tiny Encryption Algorithm）是一种分组加密算法, 使用64位的明文分组和128位的密钥, 它使用Feistel分组加密框架, 需要进行64轮迭代, 但是作者认为32轮已经足够了

feistel

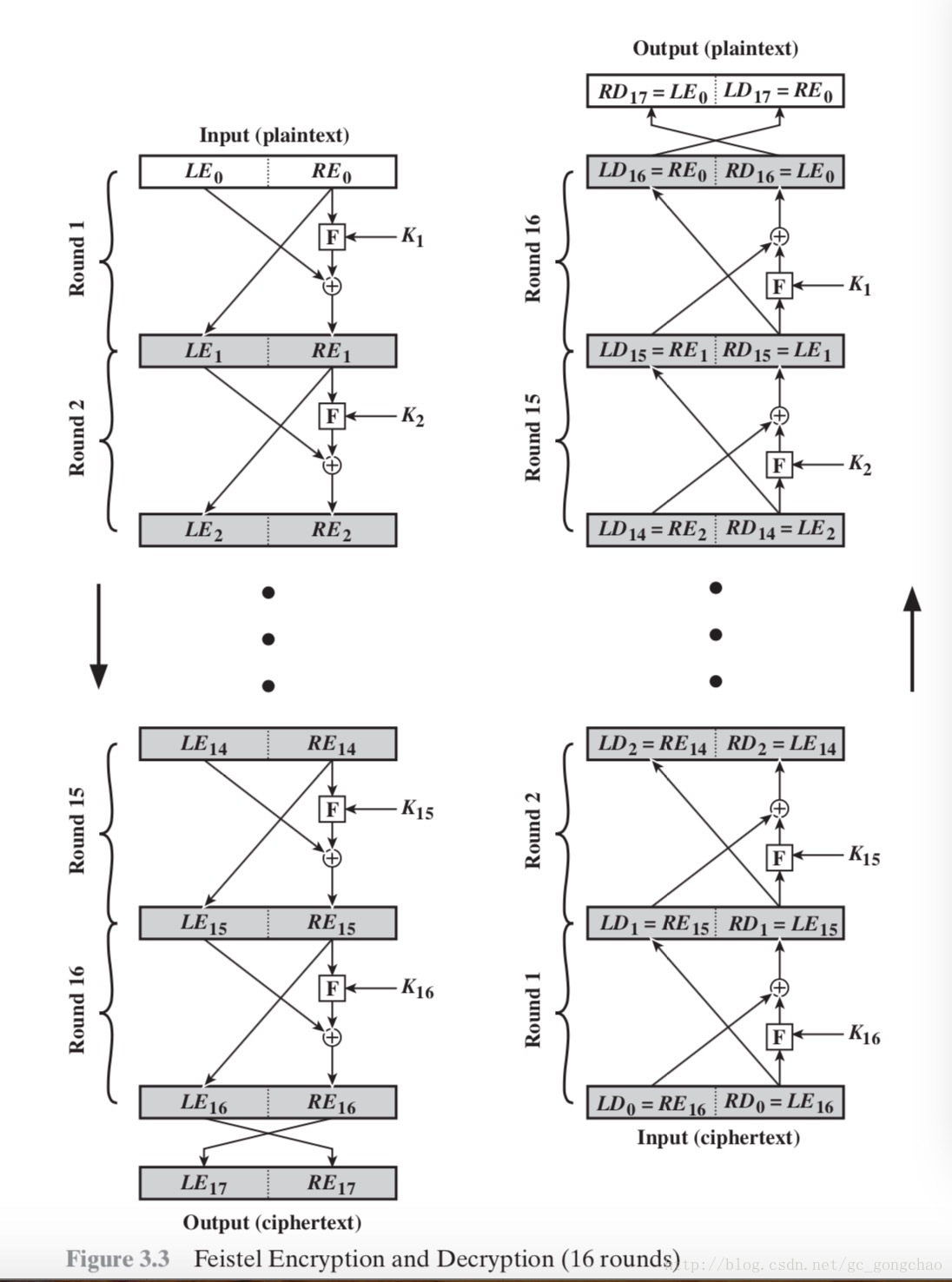
TEA加密解密是以原文以8字节（64位bit）为一组, 密钥16字节（128位bit）为一组, 该算法加密轮次可变, 作者建议为32轮, 因为被加密的明文为64位, 所以最终加密的结果也是64位

该算法使用了一个神秘常数δ作为倍数, 它来源于黄金比率, 以保证每一轮加密都不相同. 这个δ对应的数指就是0×9E3779B9, 所以这个值在TEA加密或者解密中会有用到

tea0

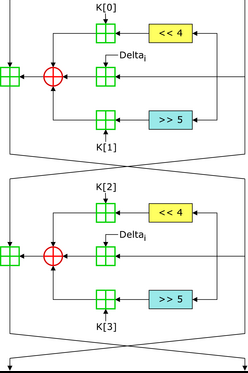
流程1：

首先TEA加密解密是以原文以8字节，所以从两边各自传入四个字节
右边传入的4个字节，这里将这4个字节称呼为M，M进行了三个部分的操作，M左移4位与密钥[0]相加，M右移5位与密钥[1]相加，M与δ相加，最后这三个算出的值再异或
左边传入的4个字节，这里将这4个字节称呼为N，N=N+M

流程2：

接着就到了下面这个部分，这里的话M和N交换了位置，

右边传入的4个字节，N进行了三个部分的操作，N左移4位与密钥[2]相加，N右移5位与密钥[3]相加，N与δ相加，最后这三个算出的值再异或
左边传入的4个字节，M=M+N

此时拿到的M和N就是加密过后的M和N

C程序实现:

1
#include <stdio.h>
2
#include <stdint.h>
3

4
void tea_encrypt(uint32_t* v, uint32_t* k) {
5
    uint32_t v0 = v[0], v1 = v[1], sum = 0, i;
6
    uint32_t delta = 0x9e3779b9;
7
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
8
    for (i = 0; i < 32; i++) {
9
        sum += delta;
10
        v0 += ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
11
        v1 += ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
12
    }
13
    v[0] = v0; v[1] = v1;
14
}
15

11 collapsed lines
16
void tea_decrypt(uint32_t* v, uint32_t* k) {
17
    uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, i;
18
    uint32_t delta = 0x9e3779b9;
19
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
20
    for (i = 0; i < 32; i++) {
21
        v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
22
        v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
23
        sum -= delta;
24
    }
25
    v[0] = v0; v[1] = v1;
26
}